An Applied Approach to Film Formation The Glass Transition Temperature Evolution of Plasticized Latex Films

In coatings science the understanding and modeling of film formation are paramount to the rapid optimization of waterborne formulations. This proves especially true in the design of coatings with targeted properties that meet required VOCs. In 1946 when Dow Chemical Co. first introduced latexes to the coatings market, there was an immediate need for understanding film formation from waterborne polymeric particles.1 Initial theories of film formation focused on particle deformation. In the dry-sintering theory proposed by Bradford and coworkers,2 the major contribution that drives particle deformation to a fully dense film arises from the surface tension of the polymer.3 According to Brown,4 particle deformation resulted from the capillary forces, which develop at the surface of a drying latex. These forces were estimated as being proportional to the water-air interfacial tension and inversely proportional to latex particle size. Vanderhoff proposed that water interfacial tension provided the force necessary for particle compression and densification.5 Sheetz suggested that the evaporation of water from latex films resulted in stresses that compressed the particles.6
Voyutskii was the first to suggest that autohesion or polymer diffusion was necessary to develop mechanical properties.7 He referred to autohesion as a mechanism that leads to the healing of weak particle boundaries. Indirect evidence for this type of molecular re-arrangement or polymer diffusion has been obtained. Studies by electron microscopy show that after latex particles compact and densify, the evolving cells continue to change, leading eventually to a continuous, smooth film.2,8 Surface-force microscopes such as atomic force microscopy, first applied to latex films in 1992 showed that a film surface flattens with aging.9
During the 1980s and '90s, direct measurement of the diffusion of polymer chains in latex films became possible through the application of two spectroscopic techniques: small angle neutron scattering (SANS) and direct non-radiative energy transfer (DET). Hahn et al.10 and Sperling et al.11 monitored the diffusion of deuterated poly(butyl methacrylate) and deuterated polystyrene, respectively, using SANS. More recently, Winnik and coworkers at the University of Toronto12 developed the DET method for diffusion measurements of latex polymers. These techniques allow one to correlate the diffusion of polymer molecules across the intercellular boundaries in a latex film with the development of the mechanical strength of the film. In fact, estimates for the amount of interparticle volume fraction of mixing, i.e., film formation, were obtained.
In the early 1990s, Winnik et al. published a classical paper demonstrating film formation for poly(butyl methacrylate) latexes in the presence of solvents.13 The addition of solvents such as Texanol_ to a waterborne poly(butyl methacrylate) latex was shown to increase the interparticle polymer chain diffusion in a predictable manner. Increasing the absolute difference between the Tg of the plasticized film and cure temperature was also shown to increase the rate of polymer chain diffusion from one particle to another.
In addition to academic studies of film formation, there have also been some important attempts by the coatings industry to develop applied film formation models. Hoy introduced the relationship between minimum filming formation temperature (MFT), Tg of the filming aids, and the distribution of filming aid between the water phase and polymer.14 However, the Tgs of only a few filming aids were measured. Using Hoy's approach, the Coatings Research Institute in Belgium demonstrated a simplified film formation model for latexes.15 However, no attempt was made to take the evaporation of solvents into account. On the other hand, Stratta, Dillion, and Semp (SDS) at Union Carbide Corp. developed the first principles to model the "wet-stage evaporation" of homogeneous waterborne polymers.16 Their work measured solvent volatility in aqueous systems, thereby accounting for the influence of activity coefficient, air velocity, temperature and composition. Still, a unified, applied film formation model that could aid the formulator in the selection of filming aids for water dispersions of polymeric particles does not exist.
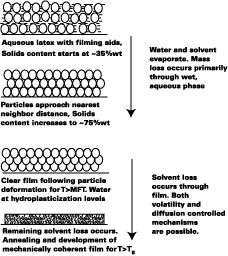
Film Formation Model
Since the Tg of plasticized latex films plays such an important role in the diffusion of polymer molecules across the intercellular boundaries in latex films, the primary purpose of the film formation model presented in this work is to predict the Tg of plasticized latex films with time. The model, while borrowing from the work of pioneers, attempts to further the understanding of film formation by systematically treating the important stages and mechanisms of film formation at the macroscopic level. Figure 1 illustrates the film formation process for latex systems formulated with filming aids.As shown by Winnik, the time at cure temperature and difference between the cure temperature and Tg of the polymercontrols the rate of polymer chain mixing from one particle to another in latex films. In Figure 1, this process begins at particle deformation. The main focus of the model presented in this work is to predict the Tg of latex films as a function of time. This article is divided into the following sections.
- 1. The use of the non-volatile plasticizer, tributoxyethyl phosphate, commercially known as KP-140_ is used to study a simple latex system. The MFTs and Tgs of clear films from the model latex are shown to obey the Hoy modified Fox-Flory equation at particle deformation and beyond. To use the Hoy modified Fox-Flory equation, the Tg of the filming aid must be known. The Tgs of commercially available filming aids are reported.
2. Next, methods and factors necessary to model volatile filming aids are considered. For the purposes of this article, this step begins following formula application to the point of particle deformation (see Figure 1). MFT measurements are used to calculate the amount of solvent in the film. The Stratta, Dillion and Semp rate equation is introduced. The use of this equation allows "average" activity coefficients for solvent loss during the wet stage evaporation to be determined. Relative evaporation rate (RER) values are reported for commonly used filming aids in the coating industry. The concept of distribution coefficients is discussed. The use of activity coefficients to predict filming aid loss during wet stage evaporation is demonstrated.
3. It is shown that a suitably formulated acrylic latex often exhibits first-order volatility-controlled solvent loss, followed by diffusion-controlled loss. The half-lives of selected commercially available filming aids are reported. The Tg evolution of a latex film prepared from a formulation of the experimental latex that contains five filming aids is demonstrated. As an indicator of the influence of composition, we will test and use the Hoy modified Fox-Flory equation to model the film's glass-transition temperature. Examples of non-volatile and volatile solvents are used to illustrate the principles.
Experimental DSC of Filming Aids
Tg measurements were made on a TA Instrument, model # DSC 2910. Typically, samples were quenched from room temperature to -150 deg C in about 7 minutes. The DSC sample temperature was ramped to 50 deg C at a rate of 15 deg C/min. The midpoint in the transition of the DSC plot is reported as the Tg of the solvent.
DSC of Latex Films
To obtain the Tg of polymeric films containing KP-140 (see Figure 2), it was added with stirring to the latex and the formulation allowed to equilibrate overnight. Samples were then cast over Teflon film and allowed to air dry until a clear film formed. The clear films were then submitted for DSC analysis. For films that contained Texanol, samples were cast over Teflon film, air dried until a clear transparent film formed, then stored at temperatures <5 deg C until DSC analysis.MFT Measurements
MFT measurements were made on a minimum film-forming temperature bar designed by Paul Gardner Co. Films were typically cast using a 76 mm gap bar. Films were allowed to equilibrate for 30-60 min. The temperature measurements were made at the cloudy (or cracked) film to clear and continuous film transition using a thermometer probe, model 874F designed by TEGAM Inc. During the measurements, moisture was removed from the film's environment by passing air over the wet film. The humidity of the air varied between 40% and 60% RH.Preparation of the Styrene/Ethyl Acrylate (SEA) Latex
The latex was prepared by semi-batch emulsion polymerization using a surfactantless process. The composition of the latex was styrene/ethylacrylate/hydroxyethylacrylate/ methacrylic acid: 40/54/3/3. The latex was filtered through a 100-mesh wire screen. Dried solids, 100-mesh screen, < 0.001%; solids, 42.61%; pH, 8.94; Mn, 20,960; Mw, 256,600; particle size, 140 nm (Dn); Tg, 41 deg C; MFT, 34 deg C.Distribution Coefficient Measurements
A 100 g sample of the SEA latex was formulated with ~20 g of water and 16 g of a single solvent under agitation. After setting overnight, the formulation was centrifuged in a Beckman L8-70 ultracentrifuge at 30,000 rpm for 20 hours at 22 deg C. Next, the samples were allowed to equilibrate in a constant temperature room (22 deg C) for 4 hours. Finally, the supernatant from each centrifuge tube was submitted for GC analysis with the amount of solvent quantified according to a GC calibration plot.Solvent Loss from Films
Dried films of the model latex were prepared on Al panels at measured film thickness and mass. The films were then uniformly dosed with a single solvent, placed in a sealed container with additional solvent not in direct contact with the film, and allowed to equilibrate for at least 48 hours. The panel was then pulled and set out at laboratory conditions, where its mass was recorded with time.Understanding the Case for a Non-Volatile Filming Aid
Figure 1 depicts the film-formation process for the purposes of this article. We are particularly concerned with determining the Tg of the latex at the time of particle deformation because (a) interparticle polymer chain diffusion begins, (b) the rate of polymer chain diffusion from one particle to another depends upon the difference between the cure temperature (22 deg C in this work) and the Tg (or MFT) of the film, and (c) MFT measurements can be used to estimate the temperature necessary for particle deformation. We first begin by describing some of the important parameters needed to model the case of a non-volatile filming aid (true or quasi-plasticizer) in a latex. In this exploratory work the effects of Tg and MFT depression are measured using two solvents, KP-140 and Texanol, which plasticize the styrene/ethyl acrylate based latex (SEA latex).Hoy modified the Fox-Flory equation for use with polymers and filming aid,
The Vp and Vs are the volume fractions of polymer and filming aid, respectively, and Tgp and Tgs are the glass-transition temperatures of the polymer and coalescing aid, respectively. Tg is the glass transition of the plasticized system, and the a value is a factor accounting for small changes in plasticizing efficiency as compared to an internally plasticizing co-monomer in the polymer.14
DSC was used to determine the Tg of 29 solvents. The Tg results are shown in Table 1. The midpoint on the DSC plot is the reported result for the Tg of the solvent. Results varied from as high as -67 deg C to as low as -129 deg C. The average Tg value is -96 deg C for all the solvents listed in Table 1. The only requirement for determining the Tg of a filming aid is that it can be frozen in the amorphous state. Filming aid Tg values reported by Hoy and the Coating Research Institute (CRI) are also listed.
Since the Tg of water cannot be measured, its effect on the film formation process is determined by measuring the minimum film-forming temperature of a particular polymer. On an MFT bar, this temperature is taken where the film transitions from clear and continuous to cloudy and cracked. It is hypothesized that this transition also closely corresponds to the point where particle deformation is reasonably complete. A reduction of the MFT below the Tg of the polymer is due to the hydroplasticization effect of the water.17


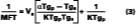
Formulations of the SEA latex with KP-140 were used to explore the validity of the above Fox-Flory Equations (Eq. 1 and 3). The plots in Figure 2 show that Eqs. 1 and 3 follow the Fox-Flory-Hoy equation. For the Tg Fox-Flory-Hoy plot, linearity was maintained up to 40 phr of KP-140. The fact that the plots are parallel suggests that K in Eq-2 is a constant for this system. The Tg and MFT of this polymer were determined to be 41.4 deg C and 34.1 deg C, respectively.
Alpha Values
Since KP-140 has an extremely low vapor pressure, and film measurements showed no loss of the solvent from films within one week by DSC and gravimetry, it is straightforward to determine an a value for a latex-KP-140 system. The a values from the Tg and MFT Fox-Flory-Hoy plots are essentially the same, 1.01.Fox-Flory-Hoy plots were also obtained for the SEA latex formulated with Texanol. The a value (1.014) obtained from the Tg Fox-Flory-Hoy plot obtained using Texanol as the filming aid is essentially the same a value (1.009) obtained from the Tg Fox-Flory-Hoy plot using KP-140. On the other hand, the a values obtain from MFT Fox-Flory-Hoy plots had less agreement, 1.01 for KP-140 vs. 1.05 for Texanol.
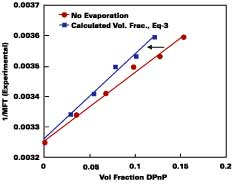
Modeling of Wet-Stage for Volatile Solvent Case
In practice, solvents used to plasticize a waterborne polymeric particle are also volatile. A method was sought that could predict the amount of solvent loss from the beginning of the drying process to particle deformation. Figure 3 illustrates the necessity for considering volatility for the common cosolvent DOWANOL DPnP. In this experiment, the MFT for a series of increasing levels of DPnP formulated with the SEA latex was recorded. A plot of 1/MFT vs. the volume fraction of DPnP in the latex film is given according to two models.The bottom line assumes no evaporation of solvent, whereas, in the top line, the volume fraction of solvent in latex film is calculated using the Hoy-Fox-Flory equation (Eq. 3, a = 1.01). The difference between the two curves is directly attributable to the amount of solvent loss from point of application to particle deformation. Conversely, it should be obvious from Figure 3 that if the volume fraction of DPnP in the latex films were known in advance, by calculating the amount of solvent loss, then the 1/MFT values could be calculated from Eq. 3.
To account for solvent and water evaporation in a latex system, we used a modified form of the SDS equation
Most of the usual definitions are retained: is the rate of evaporation of water (2.58 g/min-m2 at zero air velocity and 25 deg C); Xi is the initial mole fraction of solvent i in the aqueous phase, and Xw is the initial mole fraction of water; gi is the activity coefficient of solvent i, and gw is the activity coefficient of water; hw is the relative humidity of water. The determination of Xi and gi values for filming aids typically used in the paint industry is discussed in the sections below.
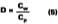
Determination of Xi
The mole fraction of solvent in the water phase is determined from the distribution coefficient (D) which, for this work, is defined according to Hoy:Cw is the concentration of solvent in aqueous phase (grams of solvent per grams of water) and Cp is the concentration of solvent in the latex particles (grams of solvent per grams of polymer). We will assume that the distribution coefficients used for the calculations in this study are nearly independent of absolute concentration in the formulated latex. The amount of solvent in the water phase at time of formulation can be calculated from the distribution by:
where Mt is the total mass of solvent added to the latex and St is the percent solids of the latex.
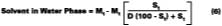
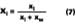
With no allowance for variation in latex composition, the fit shows that 91% of the distribution coefficient can be correlated to the hydrogen bonding solubility parameter, dhw, of water and the solvent, dhs. Strongly supportive of Hoy's arguments, it is remarkable that the distribution coefficient depends mainly on the interaction between the filming aid and the water phase and not the interaction between the filming aid and polymer.
Evaporation Rate Constants
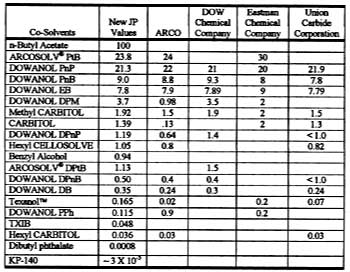
Solvent evaporation rates [mass/(area x time)] are customarily normalized to the solvent evaporation rate for n-butyl acetate. With n-butyl acetate assigned an RER of 100, the value for a pure solvent is related to its relative evaporation rate (RER) by,where the constant 0.0186 is the experimentally determined rate of evaporation of n-butyl acetate at 22 deg C.16 Table 3 shows commercially available RER values from DOW, Eastman Chemical Co. and the former Union Carbide Corp. (now part of DOW), and ARCO (ARCO's t-butyl propylene glycol-based solvents are now sold by Lyondell). It is seen that many of these RERs do not agree from one company to the next and often have just one significant figure. To obtain accurate values, this laboratory determined new RERs for typical solvents at 22 deg C under constant laboratory conditions. These values are shown in Table 3.
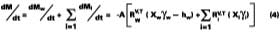
Solving Equation 4 for t
A simple solution to Eq. 4 is obtained by assuming that (a) the evaporation of water defines the boundary for the wet-stage, (b) that the water evaporates at a constant rate, and (c) that as the water evaporates, any filming aid continually maintains its original distribution between the water and polymer phases. Controlled experiments in our laboratory show that when 3.2 wet-mil films of the SEA Latex formulated with 5 phr of KP-140 at 33.8% solids were cast over CRS panels, the amount of water detectable by gravimetric analysis is 2.7% (range 2.5-2.9%) at dry-to-touch (~ 1 mil dry). The first and third assumptions above are tantamount to stating that any solvent located in the interstitial spaces of the latex particles is squeezed into the particles during particle deformation. With known activity coefficients, solvent rates of evaporation, and distribution constants for calculating the mole fractions, it is possible to determine the amount of solvent loss which occurs from the beginning of the drying process to particle deformation. By making the assumptions previously stated, the effect of solvent on the wet-stage can be ignored, and Eq. 4 may be integrated and solved for at the point where the amount of water falls to its hydroplasticization value. Previously, it was stated that ~97 % of the water is lost from the start of evaporation of water to particle deformation. This statement has the effect of setting Mw - the amount of water released to the air - to slightly less than the known amount of water mass applied per unit area. From point of application (t = 0) to point of particle deformation, tdef, the wet-stage may be calculated accordingly,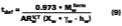

Activity Coefficient Determination
To determine the activity coefficients of solvents in the presence of water, Stratta, Dillion and Semp used the complicated Wilson expression for hydrophilic polymers dissolved in water solutions. This laboratory found this equation difficult to apply in practice. A new method that would be familiar to the paint chemist was sought. This work will show that an average activity coefficient can be determined from MFT measurements using the volume fraction versus 1/MFT relationship (Eq. 3).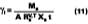
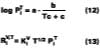
Corrections for Temperature and Air Velocity Effects
For temperature effects, the Antoine (Eq. 12), and Gardner equations (Eq. 13) are used to correct.The Antoine equation expresses the change in equilibrium vapor pressure with temperature when the Antoine constants are known for a particular solvent (see Table 4). We note that the temperature (Tc) for the Antoine equation is expressed in degrees Celsius. The Gardner equation is used to correct for temperature is defined as the mass transfer coefficient at zero air velocity (see Eq. 14) at 22 deg C and T is expressed in degrees Kelvin.
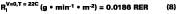
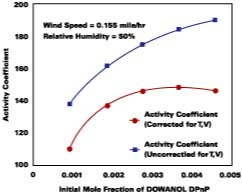
The use of Eqs. 12, 13, and 14 are explained and illustrated with examples by Stratta, Dillion and Semp.16 Here, the above equations are used to calculate values at each measured MFT. The air velocity is corrected to 0.15 miles/hr. The values are calculated and applied to Eqs. 10-11 for the calculation of the corrected gi values (bottom plot Figure 5).
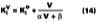
Comparative Studies of Experimental and Calculated Data
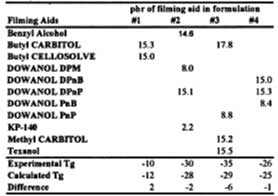
A series of formulations was prepared using the SEA latex and various levels of filming aids (see Table 5). The latex films were dried in a constant temperature humidity room (~22 deg C at 50% RH). Wet films (3.4 mils) were cast over glass plates and samples taken for DSC analysis as the wet film changed from opaque to clear. Using the activity coefficient data in Table 4 and the distribution coefficient, the Tg of these films is calculated and compared to the experimental values.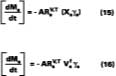
Solvent Evaporation from Films
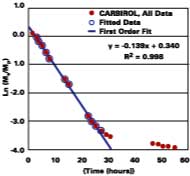
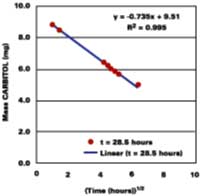
Solvent, and not heat, is used to promote the diffusion of polymer molecules across intercellular boundaries in latex films applied at ambient temperature. Ideally, a total loss of solvent to the surroundings is accompanied by a complete loss of the system's starting particle identity, thereby ensuring a maximum in properties such as hardness, chemical resistance, and mechanical strength. It is therefore equally important to understand the mechanisms governing the development of film in its latter state. The following section shows evidence that latex films plasticized with volatile filming aids first pass through a volatility-controlled solvent loss state, and then the well-known diffusion controlled state.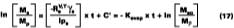
The only difference from the general equation presented earlier, is that the activity this time, (xsgs), is the mole-fraction of the solvent multiplied by the activity coefficient for a polymer-solvent system only. As often the case in polymer science, because of the disparities in molecular weights, properties of a substance are more conveniently modeled in terms of volume fractions.
Before integrating, the following substitutions should be recognized:
which is simply the volume of solvent divided by the total volume (volume of solvent plus polymer), the area A = Vt/l, and finally a replacement of Vs with Ms/rs (where rs is the solvent density). Upon integrating, and choosing the boundary condition where the only material mass as t = Y, is polymer, Mr, we have
where Ms and Mr are the mass of solvent and polymer, respectively, in the film with time, and Mso is solvent mass at t = 0.
Thus, unlike diffusion-controlled loss, a volatile stage is characterized by a first-order evaporation rate constant that is inversely proportional to film thickness.
Discussion
In this study, we have examined the effect of Tg and volatility of filming aids on the Tg evolution of latex films. First, the Tgs of typical filming aids are found to vary from -67 to -129 deg C. Accurate RER values have been determined for commercially available filming aids. The RER values are shown to be useful for calculating the their values. Apparent average activity coefficients for the evaporation of filming aids in the presence of water are determined and used to predict the Tg of latex films using a modified form of the Stratta, Dillon, and Semp equation and the Fox-Flory equation. Finally, the loss of filming aids from post-deformation latex films is shown to consist of two stages: volatility control and diffusion control.There are a number of approximations made in the various components to the film-formation model presented here. Undoubtedly, many of the coefficients, a and D, for example, may show variations with solvent levels. It is thought, however, that many of these unknowns partially cancel, and moreover that the uncertainties are incorporated in the derived wet-stage activity coefficients. Nevertheless, it is heartening that the magnitude for the gi reported here are in excellent agreement with those reported by Stratta, Dillion and Semp.16
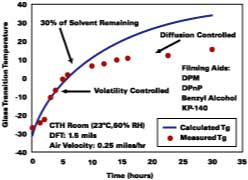
This information is now used to show the predictability of all aspects of the model for a SEA latex formulated with four solvents. The film is cast over glass in a constant temperature humidity room and the Tg of the film determined by DSC. The results are shown in Figure 8. The solid line is the Tg evolution of the film predicted by the models in this work up to and including the equation for volatility control. Diffusion control is not accounted for in this work. The calculated curve shows that the model gives reasonably good predictions up to 7 hours. We attribute the deviation between model and experiment, observed to begin at ~7 deg C, as the point where the solvent loss mechanism switches to diffusion-controlled. Here, the difference between ambient temperature and the Tg at the change from volatility control to diffusion control is about 17 deg C.
A paint formulation (formulated for maintenance coatings) prepared from the SEA latex and the filming aid selection shown in Figure 8 gave more than 200 hours of salt-fog resistance for a
1-mil coatings (dry thickness) prepared over cold roll steel. The total solvent or VOC level at 16% pigment volume concentration was 250 g/liter. Controlled experiments in our laboratory showed that when the difference between ambient temperature and the initial Tg of the coating was less than 50 deg C, a significant decrease in salt-fog resistance (corrosion resistance) was observed. We postulate that interparticle polymer chain diffusion is essentially complete before the onset of diffusion control. This postulate supports conclusions based on DET results that show that for cure temperatures greater than 50 degrees above the Tg of high-molecular-weight PBMA-based particles (Mw = 430,000), interparticle polymer chain diffusion is essentially complete within 100 minutes.12 For maintenance coatings that dry or cure at ambient temperatures, the data illustrates the difficulty in designing waterborne thermoplastic acrylic polymers that perform adequately for their targeted environment at VOC levels < 250 g/liter. For this coating application, a thermoplastic polymer with a Tg > ~28 deg C is necessary to develop adequate hardness.
Lowering the Tg of the polymer lowers the required level of solvent in the formulation, but results in a maintenance coating that does not develop adequate hardness.
Acknowledgements
Our thanks to Mitch Winnik, professor at the University of Toronto, and Ken Hoy, retired research fellow from Union Carbide Corp., for their inspiration and guidance during this work. Also, our thanks to Mike Patterson, Dennis Wilson, and Wilson Neson at Johnson Polymer who provided the leadership and funding for this work.
This article was presented at the International Waterborne, High Solids, and Powder Coatings Symposium, sponsored by The University of Southern Mississippi Department of Polymer Science, 2002, in New Orleans.
For more information on film formation, contact J.W. Taylor and T.D. Klots, Johnson Polymer, P.O. Box 902, Sturtevant WI 53177-0902; phone 262/631.4044.
References
1 (a) Lee, Do Ik, Senior Scientist Dow Chemical Co., Private Communications 1999, (b) Thompson, S. J.; The S/B Latex Story; Recollections of "Can Do" at Dow, Dow Chemical Co., 1980.
2 Henson, W.A.; Taber, D.A.; Bradford, E.B. Ind. Eng. Chem. 1953, 45, 735.
3 Dillion, R.E.; Matheson, L.A.; Bradford, E.B. J. Colloid Sci. 1951, 6, 108-117.
4 Brown, G.L. J. Polym. Sci. 1956, 22, 423-434.
5 Vanderhoff, J.W.; Tarkowski, H.L.; Jenkins, M.C.; Bradford, E.B.J. Macromol. Chem. 1966, 1(2), 361-397.
6 Sheetz, D.P. J. Appl. Polym. Sci. 1965, 9, 3759-3773.
7 Voyutskii, S. Autohesion and Adhesion of High Polymers, Wiley-Interscience, NY, 1963.
8 Wang, Y.; Kats, A.; Juhu deg , D.; Winnik, M.A.; Shivers, R.; Dinsdale, C, Langmuir 1992, 8, 1435-1442 (1992).
9 (a). Wang Y.; Juhue, D.; Winnik, M.A.; Leung, O.M.; goh, M.C. Langmuir, 1992, 8, 760-762, (b). Goh, M.C.; Juhue, D.; Wang, O.; Winnik, M.A. Langmuir, 1993, 9, 1319-1322.
10 Hahn, K.; Ley, G.; Schuller, H.; Oberthur, R. Colloid & Polym Sci. 1986, 264, 1092-1096.
11 (a) Linn deg , M. A.; Klein , A.; Miller, G.A.; Sperling, L.H. J Macromol Sci-Phys 1988, B27 217-231; (b) .Yoo, J.N.; Sperling, L.H.; Glinka, C.J.; Klein, A. Macromolecules 1990, 23 3962-3967
12 Zhao, C.L.; Wang, Y.; Hruska, Z.; Winnik, M.A. Macromolecules 1990, 23, 4082-4087.
13 Winnik, M.A.; Wang, Y.; Haley, F.J. Coatings Technol. 1992, 64(811), 51-61.
14 Hoy, K.J. Paint Technol., 1978, 45(579), 51-56.
15 Toussanit, A.; Wilde, M.De.; Molenaar, F.; Mulvihill, J. Prog. Org. Coating, 1998, 30, 179.
16 Stratta, J. J.; Dillon, P.W.; Semp, R.H. J. Coatings, Technol. 1978, 50(647), 40-47.
17 Sperry, P.R.; Snyder, B.S.; O'Dowd, M.L.; Lesko, P.M. Langmuir 1994, 10, 2619-2628.
18 Crank, J., The Mathematics of Diffusion, 2nd ed., Oxford University, 1975, Chapter 9.
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!




