Keeping You in Suspense!
The innovation of new products, whether to meet customer requirements, financial targets or environmental legislation, stimulates a constant cycle of formulation and re-formulation within the industry and creates a demand for effective and supportive analytical strategies. Within this context, this article examines the application of a trio of materials characterization techniques: particle sizing, rheological analysis and zeta potential measurement, focusing in particular on their use in the development of product stability. While it is possible to adopt a ‘trial and error’ approach to formulating, applying these analytical techniques enables more efficient, targeted product development.
Setting Formulation Targets
In an ink or coating, the particle size of the dispersed solid is one of the primary variables used to achieve desirable performance. Particle size influences the way in which light interacts with the finished coating, and therefore affects the hue or tint achieved, as well as other aspects of film appearance such as transparency and/or gloss level. Apart from the aesthetics, particle size may also impact more practical features such as weather resistance and stability.
During manufacture, particle size can also be important. Finer powders tend to be more cohesive and difficult to handle, for example. Of arguably much greater importance though is the impact that particle size has on the properties of the suspension, once the carrier and suspended solid are mixed. Particle size affects the rheology of a suspension, most especially its viscosity, which in turn has an impact on performance characteristics, such as application ease, propensity to slump or curtain, cure behavior and product stability.
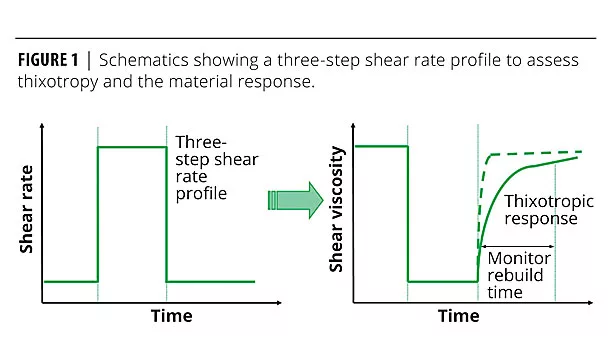
A successful formulation relies on reconciling the rheological properties of the suspension with the expected application. Consider, for example, the rheological phenomenon of thixotropy. Certain suspensions, as exemplified by many paints, shear thin, i.e., they exhibit lower viscosity when subject to higher levels of shear. When the applied level of shear is reduced, viscosity returns to a higher level but over a finite period of time (Figure 1). The longer this process takes, the more thixotropic the suspension.
With a thick coating, appreciable levels of thixotropy may be advantageous. Low viscosity will be maintained for long enough, post application, to enable brush marks to flow away, giving a smooth surface coating. On the other hand, for an ink in a printer, thixotropy may be disastrous. Once applied, the ink must stay put to give high resolution, making the instantaneous attainment of high viscosity preferable.
Successful formulation therefore demands tailored rheological characteristics to deliver a product that is easily applied, gives a high-quality finish and is stable. This last issue of stability is crucial, and is often one of the most time-consuming aspects of development. For a suspension to be functional it should maintain the dispersed phase in a suspended state for the lifetime of the product, under all relevant conditions, and/or enable easy re-dispersion should settling occur. Settling or sedimentation is problematic because it introduces the risk of non-homogeneity in a product, poor handling and a sub-standard finish. The particle size of the dispersed solid, the viscosity of the continuous phase and the rheology of the suspension can all be manipulated towards better stability, but there is one further parameter that can also be extremely useful in stability assessment and control: zeta potential.
Understanding Suspension Stability
A number of factors contribute to dispersed phase stability, and these may be classified as either kinetic or thermodynamic in origin. Kinetic stability is facilitated by increasing the viscosity of the suspending medium, thus slowing down particle movement, aggregation and sedimentation. Thermodynamic stability on the other hand relies on the manipulation of steric and electrostatic effects, the induction of stability through particle repulsion, either through size or shape modification, or by altering electrostatic charge, respectively. Zeta potential quantifies the magnitude of the electrostatic repulsion or attraction between particles and can therefore be used to study and control this aspect of stability.
In a sub-micron suspension Brownian motion is usually significant in maintaining the particles in a dispersed phase. However, for larger particles the effect of gravity becomes significant if there is a sizeable difference in density between the dispersed and continuous phases. The ratio of gravitational to Brownian forces correlates with the likelihood of sedimentation, which can be predicted from equation 1,1
a4 ∆rg
kB T [1]
where a is the particle radius, Dr is the density difference between the dispersed and continuous phases, g is acceleration due to gravity, kB is the Boltzmann constant and T is the temperature.
If this ratio is greater than unity, then some degree of sedimentation can be expected; a ratio of less than one is indicative of a stable system. However, this equation does not take into account the possible impact of particle-particle interactions. The constant collision of small particles raises the possibility of flocculation and transition to a gravity-dominated system with the attendant increase in likelihood of sedimentation. This effect is predictable from equation 1, from the increase in a, the particle radius, that flocculation would cause.
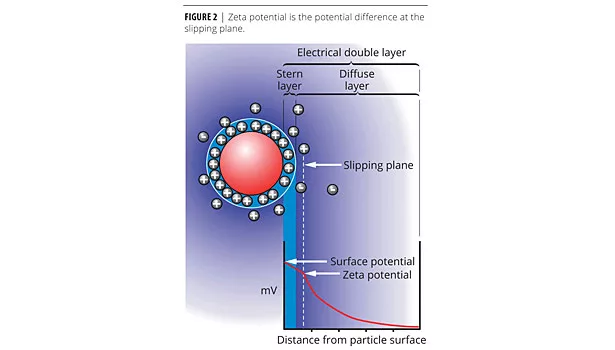
In an electrically charged suspension, DVLO (Derjaguin, Landau, Verwey and Overbeek) theory2,3 suggests that an energy barrier resulting from the repulsive force between two particles will prevent them from approaching one another and adhering, unless the particles have sufficient thermal energy to overcome it. Zeta potential, the potential at the slipping plane between the particle and associated double layer, and the surrounding solvent, indicates the magnitude of this barrier and the impact of strategies applied to modify it, such as the alteration of pH (Figure 2).
If a suspension has a large negative or positive zeta potential, then the particles within it will tend to successfully repel each other; low zeta potential values, in contrast, increase the likelihood of flocculation. The dividing line between stable and unstable suspensions is generally taken as ±30 mV; systems, with zeta potentials outside of these limits, indicate a stable system.4,5 This assumption is however dependent on particle properties.1,2
In summary, the measurement of zeta potential brings detailed insight into electrostatic dispersion mechanisms, supporting this aspect of dispersion control. Rheological measurements on the other hand facilitate the optimization of kinetic stability. These two analytical technologies are therefore complementary, and when used together enable a thorough understanding of all the factors influencing suspension stability, thereby enabling better control. The following case study shows how zeta potential and rheological analysis can be applied in combination to induce stability in a suspension of particles of defined particle size.
Case Study
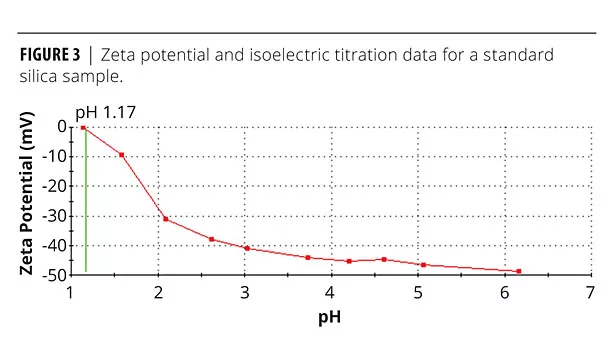
A study was done on inducing stability in a suspension of microcrystalline silicon dioxide. Figure 3 shows the effect of pH on a suspension of silica particles with an average particle size of 3.7 µm. The data were gathered using a Malvern Zetasizer Nano S in conjunction with an MPT2 autotitrator. From the starting point of a dilute dispersion of the material in deionized water, the autotitrator was used to steadily decrease pH up to an end point of 1.0 using standard HCl solutions. Zeta potential measurements were made at 10 equally spaced pH intervals across the range.
Despite having a negative zeta potential in excess of 30 mV, this suspension has been shown to be unstable, forming a compact, sedimented layer upon standing. Inputting values for the relevant parameters into equation 1 gives a result of 45, confirming the likelihood of sedimentation and suggesting that gravitational forces are highly dominant. When gravitational forces driven by particle size and density dominate the system, electrostatic interactions are insufficient to provide stability, and kinetic stabilization is therefore required.
Increasing Viscosity
As noted earlier, one way to increase the kinetic stability of a suspension is to increase the viscosity of the continuous phase.
For a dilute suspension, sedimentation rate can be estimated using Stokes’ law, which states that the sedimentation velocity is inversely proportional to the shear viscosity of the continuous phase.6 This means that doubling the viscosity will halve the rate of sedimentation. Stokes law, however, is only applicable for dilute suspensions where particle interactions are minimal. Settling of concentrated suspensions is more complex due to interactions between neighbouring particles and the fact that a high particle loading leads to an increase in overall density and viscosity.
An alternative way of inducing stability in suspensions where gravitational forces dominate is by introducing a network structure that gives the system a yield stress. Systems with a yield stress remain stationary, i.e., do not flow until the applied shear exceeds a certain value. One way to achieve such structure is to gel the continuous phase through the introduction of suitable additives. Another, which may seem counter intuitive, is to reduce the repulsion between particles and actually promote flocculation in the system.
Introducing Structure
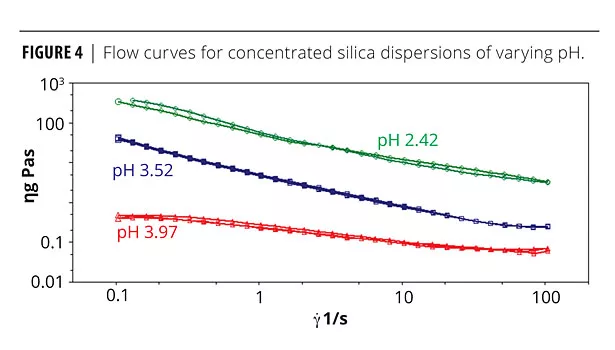
Figure 3 shows that as pH is decreased, zeta potential reduces towards the isoelectric point – the point where zeta potential is zero, which occurs at a pH of 1.17. This means that lower-pH systems will be more prone to flocculation. The effect of pH on suspension viscosity is shown in Figure 4, which displays shear viscosity as a function of shear rate (from an equilibrium step shear rate test) for concentrated silica dispersions of varying pH. All rheological data were measured using Kinexus Pro and Gemini 2 rotational rheometers (Malvern Instruments).
The data measured at a pH of 3.9 exhibit a zero shear viscosity plateau; at low shear rates viscosity attains a constant value. This shape of viscosity curve is associated with samples that are liquid-like under very low shear conditions. The curves measured at lower pH do not exhibit this feature, suggesting that at very low shear these suspensions may be more solid-like. Testing at lower shear rates would be necessary to confirm this.
In a three-step shear rate test, viscosity was measured at a low shear rate, then at a high rate and then under the original conditions (data not shown). The time taken for the suspension to regain its low-shear viscosity was measured and found to be very short, suggesting that any structure-conferring network is almost instantaneously rebuilt once high shear is ceased. These results suggest that any structure inducing flocculation within these samples is not permanent, but rather rapidly breaks down and/or reforms following a perturbation.
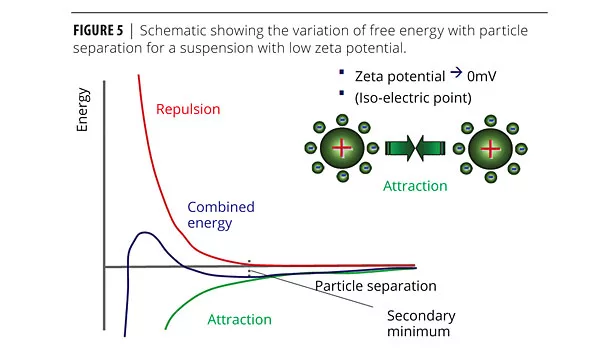
This type of reversible flocculation behavior can be rationalized using DLVO theory, which states that the combined/total energy (VT) is the sum of attractive (VA) and repulsive (VR) contributions (Figure 5). By reducing the surface charge on the particles, the repulsive contribution to the total interaction potential is reduced, creating a secondary minimum in the total energy curve that permits weak and reversible adhesion between particles. These interactions are strong enough to resist the effects of Brownian motion but sufficiently weak to be broken down under the application of shear.
In fact two forms of flocculation behavior may be observed. If the secondary minimum is relatively deep, then colliding particles will adhere strongly to form an open structure, which is favorable for network formation. In contrast, more weakly flocculated systems are able to re-arrange themselves on a local scale, forming denser flocs that are more prone to sedimentation.1,6 A greater reduction in zeta potential is favorable towards a deeper secondary minimum and the development of a network structure.
Investigating Yield Stress
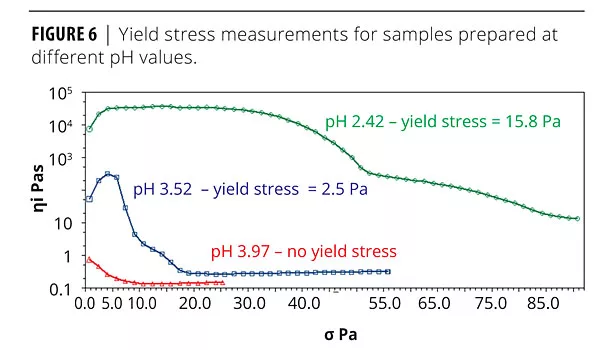
One way to investigate and quantify the impact of structure in a fluid is to measure yield stress. Yield stress is the stress required to overcome the attractive forces in the system and initiate flow. In a final series of rheological tests, the yield stress of each of the suspensions was measured by performing a shear stress sweep and determining the stress at which a peak in viscosity is observed. The results are shown in Figure 6.
The two low-pH samples show a peak in viscosity indicative of a yield stress. The stress at which this peak occurs is much higher for the low-pH sample, indicating that the structural strength developed is higher at low pH, when zeta potential is lower. For the high-pH sample there is no peak in viscosity, indicating that this material does not have a yield stress and hence no network structure. This is consistent with the viscosity curve data that shows that at this pH the suspension exhibits a zero shear viscosity plateau.
These results suggest that at lower pH, structure has been successfully induced but the question remains as to whether the attained stability levels are high enough. Equation 2 enables estimation of the stress imposed on its surroundings, by a particle, within a particulate gel,
s= (rD-rC)rg
3 [2]
where rD is the density of the dispersed phase and rC is the density of the continuous phase. Note that equation 2 is derived on the assumption that gravitational forces act over the whole surface of a spherical particle. If the gravitational force is considered to act on a normal plane, then using the cross-sectional area of the sphere, the stress imposed becomes s= (rD-rC)rg. The use of both derivations can be found in published literature.
For the silica suspension used here this calculation indicates that the largest particles present, those around 10 µm in diameter, would impose a stress of approximately 0.01 Pa. Since this figure is well below the yield stress exhibited by the low-pH suspensions, these systems should be stable under quiescent conditions. However, thermodynamic stability will only be maintained if the stress imposed on the structure is below the yield stress. Higher stresses could occur during transportation for example or during use, causing instability.
Conclusion
For a coating or ink, particle size, zeta potential and rheology are all important characteristics. The application of analytical strategies based on the measurement of all three therefore promotes knowledge-driven formulation towards a stable product that is easily applied and gives a desirable finish. All three parameters interact to confer performance on a suspension; understanding these interactions is the key to their closer control.During formulation, achieving product stability is one of the most demanding and time-consuming tasks. The case study described here shows how this task can be made easier, with a dispersed phase of defined particle size, through the application of zeta potential measurements and rotational rheometry. Recognizing the different mechanisms that control stability – whether kinetic or thermodynamic – and adopting an approach that systematically and relevantly addresses them, leads to the successful induction of sufficient stability to fulfil in-use requirements.
References
1 Larson, R.G. The Structure and Rheology of Complex Fluids, Oxford University Press, New York, (1999).
2 Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Acta Physico Chemica URSS 14, 633. (1941).
3 Verwey, E.J.W.; Overbeek, J. Th. G. Theory of the stability of lyophobic colloids, Elsevier, Amsterdam, (1948).
4 Zeta Potential in 30 Minutes, Technical Note available from www.malvern.com.
5 Zeta Potential of Colloids in Water and Waste Water, ASTM Standard D 4187-82, American Society for Testing and Materials, 1985.
6 Barnes, H.A. A Handbook of Elementary Rheology, University of Wales, Institute of Non-Newtonian Fluid Mechanics, (2000).
Looking for a reprint of this article?
From high-res PDFs to custom plaques, order your copy today!






