In his benchmark paper, P.J. Flory¹ used statistical mechanics to relate the elastic modulus of a polymer network in the rubber phase to the number of elastically effective chains and related this to the crosslink density. He also correctly taught a method to calculate the number of elastically effective chains (v) based on the molecular weight (Mn) of the rubber prepolymer and the molecular weight between reactive groups (Mc).

v = 2(number of crosslinks) = v_o(1 – 2Mc/Mn)

This Mn correction arises from the fact that some of the reactive groups on the prepolymer are used to build a chain of infinite molecular weight. At this conceptualized intermediate state of infinite molecular weight, each of the prepolymer chains has reacted with two other prepolymer chains and no crosslinking has occurred. There is only chain extension and there is only one elastically effective chain. Additional reactions will form crosslinks within this infinite chain. He notes that then ALL crosslinks are within the same (infinite) chain and the argument that intrachain crosslinks (here referring to within the same prepolymer) having a diminished value is refuted. Flory also discusses the noncontributory status of dangling chain ends in this model. However, he makes no additional correction for these chain ends in his equation relating the molecular weight of the prepolymer to modulus. In spite of this omission, he achieves excellent correlation of the number of effective chains or crosslink density and modulus and to swelling using only the correction for achieving infinite molecular weight.

Nonetheless, J. Scanlan² continued with a statistical mechanical approach to calculate the distribution of the chain ends that result during network formation. This results in only minor differences to the predictions of Flory’s original model. In this same paper, Scanlan also begins the process of calculating the probability of some reactions being nonnetwork-enhancing.

D.R. Miller and C.W. Macosko³ further extend Scanlan’s probability theory to prepolymer chains of varied degrees of functionality (f). They use a statistical mechanical foundation to derive a solution for incomplete reaction. However, at 100% reaction, their result yields the same answer as Flory’s original concept. The nonnetwork-enhancing reactions are the same ones that are required to build infinite molecular weight. Graessley⁴ validates this approach in his edition of Advances in Polymer Science.

L.W. Hill⁵ applies Scanlan’s, and Miller and Macosko’s work to thermoset coatings. However, the equations that he uses do not include the correction for infinite molecular weight. In the end he argues that the correction for the polymer degree of functionality (i.e. infinite molecular weight) may be unnecessary based on a single experimental data point.

In the meantime, Berger and Huntjens⁶ developed a simpler treatment that is close to what will be presented here.

All the treatments so far have required that the degree of functionality for each polymer in the system be a known integer. While this is always true on the molecular level, molecular weight and functional group distributions result in noninteger averages for most resins. This work will depart from the method of counting the elastically effective chains. It will instead calculate the number of crosslinks per unit weight (XLD) based on readily known resin constants. If desired, this can then be easily converted to the mols of elastically effective chains per unit volume. v/NV = 2(XLD)r, where r=density and N = Avagadro’s number. In the end, we will compare our results with those mentioned in the introduction. We will also revalidate the validity of the infinite molecular weight correction with experimental data. We will then extend these concepts to UV-cured systems and kinetic chain length.

Most of the work discussing crosslink density is made in effort to correlate with the tensile modulus of the polymer network in the rubbery region, as Flory did in 1944. In many cases, the crosslink densities of these systems are 2-3 orders of magnitude greater than those of Flory’s vulcanized polyisoprene. Yet the modulus in the rubbery plateau still correlates with estimates of the number of chains or crosslink density. The basis of Flory’s treatment showed that the configurational entropy (and hence the energy) of a long polymer chain increased linearly with the length of deformation. This is based on the fewer number of conformations that are available as the end-to-end distance in increased. The effect of this linear relationship of energy with distance is a neo-Hookean entropic spring.

While the modulus in the rubbery region is often used to measure the crosslink density, it is seldom of interest as a coating property since most coatings perform service in the glassy domain. However, crosslink density has relevance to other properties as well. Most important is the effect on the Tg due to its effect on chain mobility.⁷ Other important properties include the fracture energy^8,9 and the degree of plastic flow.¹⁰

Model for Thermoset Polymers

For thermosettable polymers, the molecular weight between reactive groups is usually known and is referred to as an equivalent weight. It is sometimes expressed in units such as acid value, hydroxyl value, weight percent hydroxyl or weight percent of NCO, etc. that can be converted to equivalent weight.

For thermosetting polymer systems, there are typically two different types of polymer with each containing a functional group that is reactive with a functional group on the other polymer type. For example, a polyisocyanate and a polyol. In calculating the number of bridges between polymer chains, each reactive group contributes ½ of a bridge. We are assuming a 1:1 stoichiometric ratio of reactive groups and we are being careful not to call the bridges crosslinks yet. Thus the number of bridges per unit weight of cured film at 100% reaction is given by Equation 1.

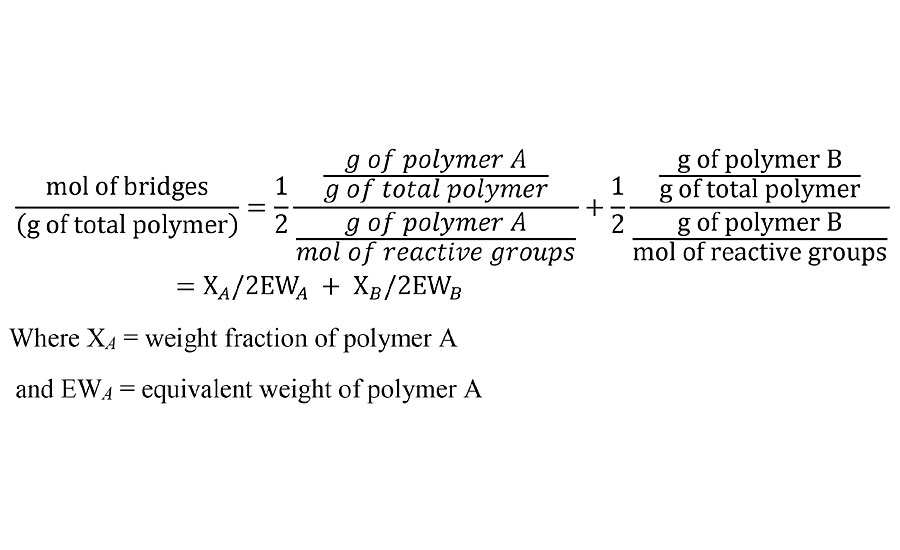
EQUATION 1 » Moles of prepolymer bridges per unit weight.

But clearly, this has no accommodation for the number of interpolymer bridges required to form the chain of infinite molecular weight. This adjustment can be made by removing two reactive groups for each polymer chain to calculate an adjusted equivalent weight EW’ as shown in Equation 2. This is done for each of the polymers in the system.

EQUATION 2 » Adjusted equivalent weight.

This is simply a stoichiometric-based equivalent of Flory’s statistical mechanical correction for infinite molecular weight. We will later confirm that this technique of removing two groups per chain is valid for various degrees of functionality in the prepolymers. A typical example for a hydroxyl functional acrylic resin of 400 EW and 2000 Mn yields and adjusted EW’ of 667g/mol.

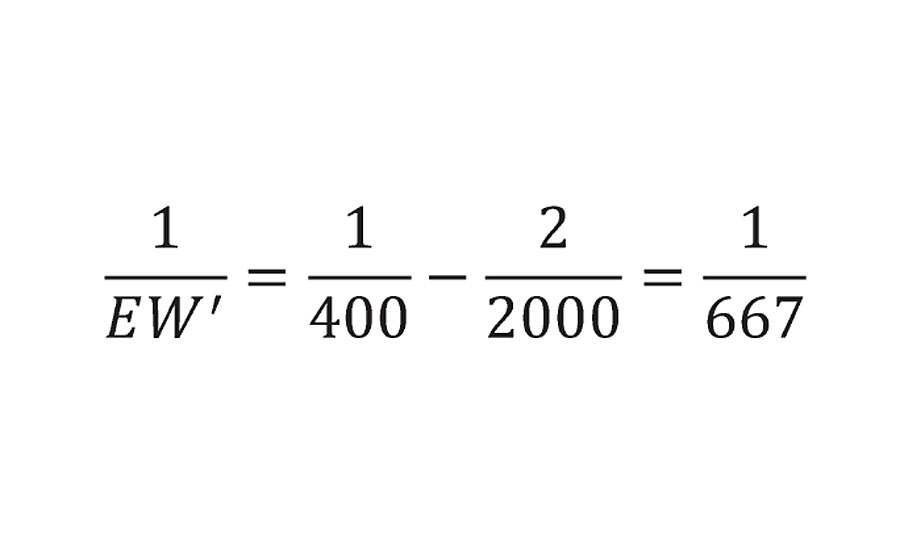
This adjusted equivalent weight can be substituted into Equation 1 to yield Equation 3.

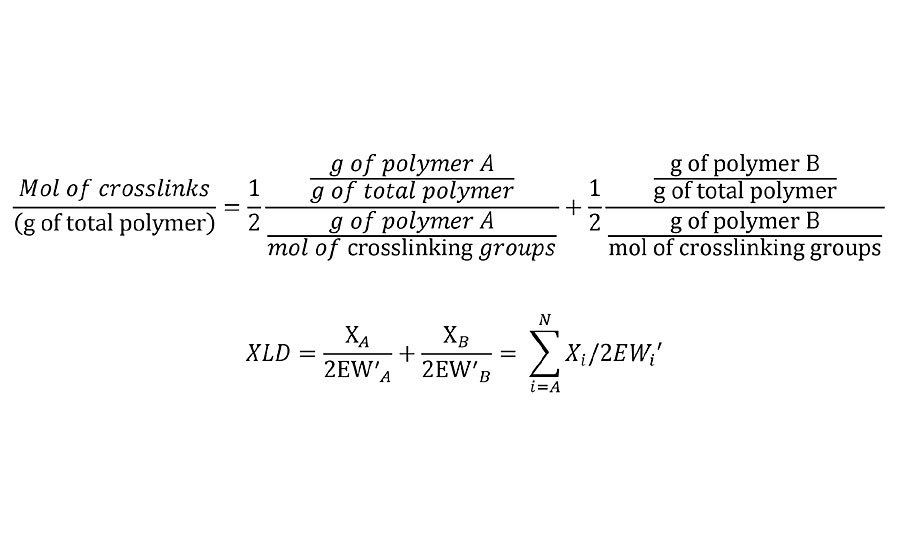
EQUATION 3 » Moles of crosslinks per unit weight.

Note that this is the mol/g of the final network. So in the case where the crosslinking reaction results in the loss of a leaving group, it is required that the weight of these leaving groups be subtracted from the Mn, from the unadjusted EW and from the weight fraction of polymer in the film. In the case of some crosslinkers such as melamines and polyisocyanates, excess reactive groups can self-condense. In such cases, excess crosslinker stoichiometry can be used in this calculation by simply adjusting the weight fractions to their nonstoichiometric values.

In cases where the reaction of a polymer is incomplete, either due to imbalanced stoichiometry or due to incomplete cure of the two polymer system, this adjustment is easily made in Equation 2. For example if the reaction is only 80% complete, then the mols of reactive groups is 0.8 times the total. Thus the first term in Equation 2 is adjusted as in Equation 4 for both polymers.

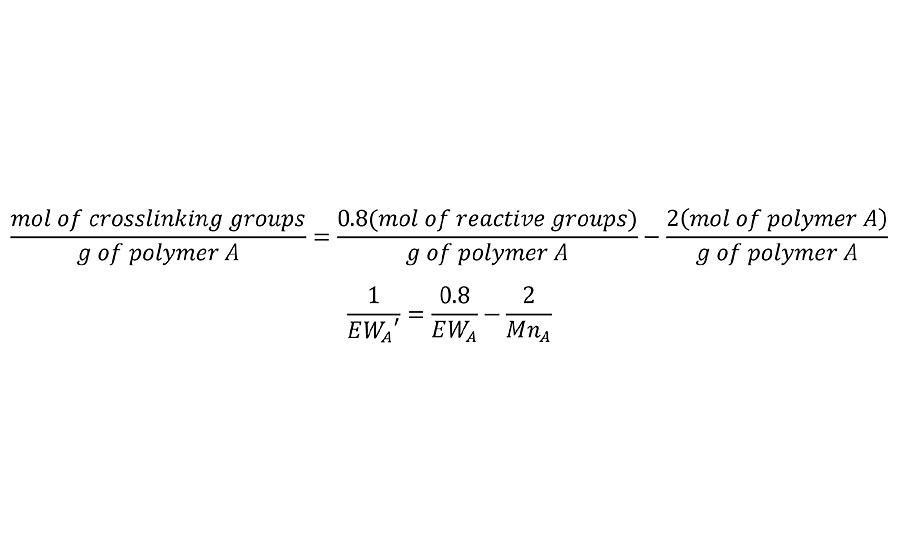
EQUATION 4 » Equation 2 adjusted for incomplete reaction.

If desired, this degree of reaction can be reduced to the limit of zero crosslink density in the system to find the degree of reaction at gel point or infinite molecular weight.

We have shown a series of simple algebraic equations for the calculation of the crosslink density that are based on readily obtained information for most polymers combined with the polymer weight fractions and stoichiometries that are known from the coating formulation. In addition, this method can be applied to cases where the average number of groups per chain is a noninteger value (as is usually the case).

We will now review a number of prepolymer chain functionality combinations to confirm that removal of two reactive groups per chain applies to all cases. In each case, we will consider the number of groups on each polymer and its influence on the building of the network to infinite molecular weight and the number of crosslinks formed.

Two Reactive Groups on Polymer A and Two Reactive Groups on Polymer B

From the discussion above, it is clear that such a system cannot crosslink. This is confirmed by the calculations in Table 1. At 1:1 stoichiometry this system can only form infinite molecular weight. Such a system represents the many thermoplastic polymers such as polyamides, (e.g. PA 6,6) and polyesters etc.

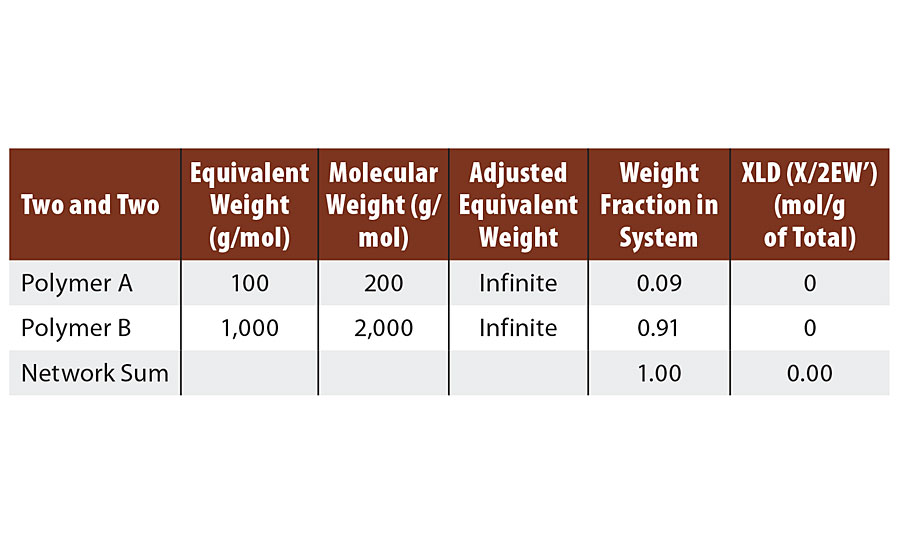
TABLE 1 » Calculated crosslink density of FA = 2, FB = 2.

Three Reactive Groups on Polymer A and Three Reactive Groups on Polymer B

This provides a straightforward example of the transition from infinite molecular weight to the crosslinked network. At 1:1 stoichiometry and ²/₃ of the groups reacted, the system has achieved infinite molecular weight with no crosslinks. The reaction of the third group from polymer A and from polymer B provide ½ of a crosslink each in the final network, as shown in Table 2.

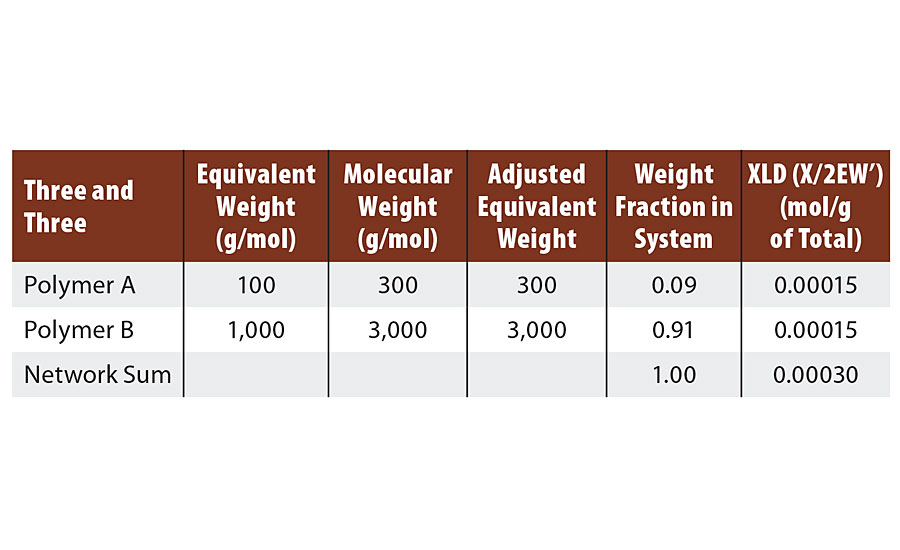
TABLE 2 » Calculated crosslink density of FA = 3, FB = 3.

This same scenario can readily be extrapolated to four groups on each chain, five groups, etc. We will now consider the case where the two polymers have a different number of functional groups.

Six Reactive Groups on Polymer A and 2 Reactive Groups on Polymer B

This system could represent a hexafunctional melamine and a polyester diol. Such a system is more challenging to conceptualize at infinite molecular weight. When each (hexafunctional) melamine has reacted twice and ¹/₃ of the diol molecules have reacted twice, there is one chain of infinite molecular weight. But there is also ²/₃ of the diol chains still unreacted since there are three times as many diol chains as melamine molecules.

If each of these remaining ²/₃ of the diols react at only one end with melamine, then infinite molecular weight and gel point are achieved. Reaction of the second end of the ²/₃ diol chains with melamine then result in crosslinks (Table 3).

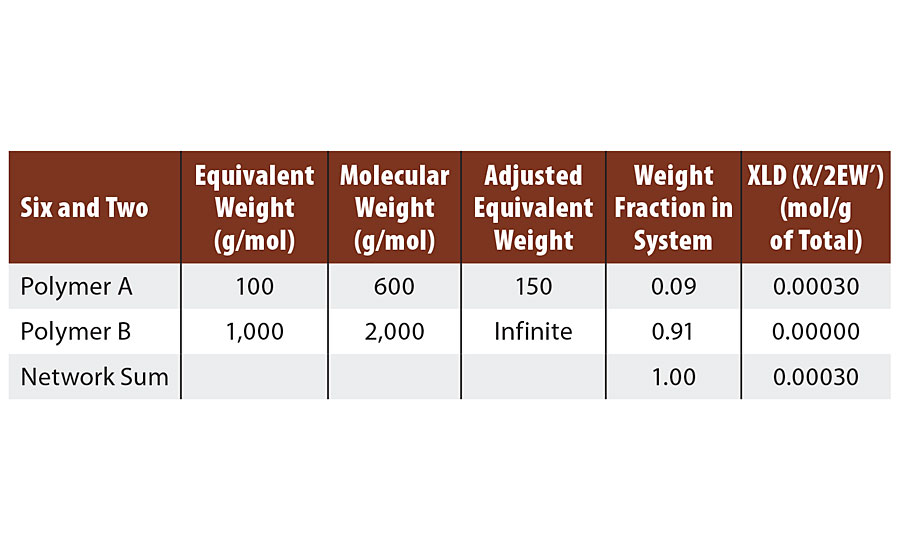
TABLE 3 » Calculated crosslink density of FA = 6, FB = 2.

The algebra treats this situation slightly differently, but the same result is achieved. We start again at the point where each melamine is reacted twice and only ¹/₃ of the diol chains are reacted. After this point, each time that a diol reacts at both ends with two different melamines a single crosslink is formed. However, the single crosslink results from the two ½ crosslinks that are provided by the two melamine molecules. None of the crosslinks are assigned to the diol molecule.

Thus the diol behaves the same way in this example as it did in the first example by contributing zero crosslinks. This provides an important learning for network design. Only chains with more than two reactive groups can crosslink. This will be true in any system that such a resin is used. However, if such difunctional chains are paired with highly functional co-reactants, then crosslinking can be achieved via the coreactant. We will now consider another imbalanced system.

Four Reactive Groups on Polymer A and Three Reactive Groups on Polymer B

At 1:1 stoichiometry, the number of chains is opposite the number of groups per chain. So there are three molecules of polymer A for every four molecules of polymer B. Thus when each molecule of polymer A has reacted twice, only ¾ of the polymer B chains have reacted twice, and there remains ¼ unreacted, as shown in Figure 1. Unreacted groups are shown as open circles and reacted groups, or bridges, are shown as closed circles.

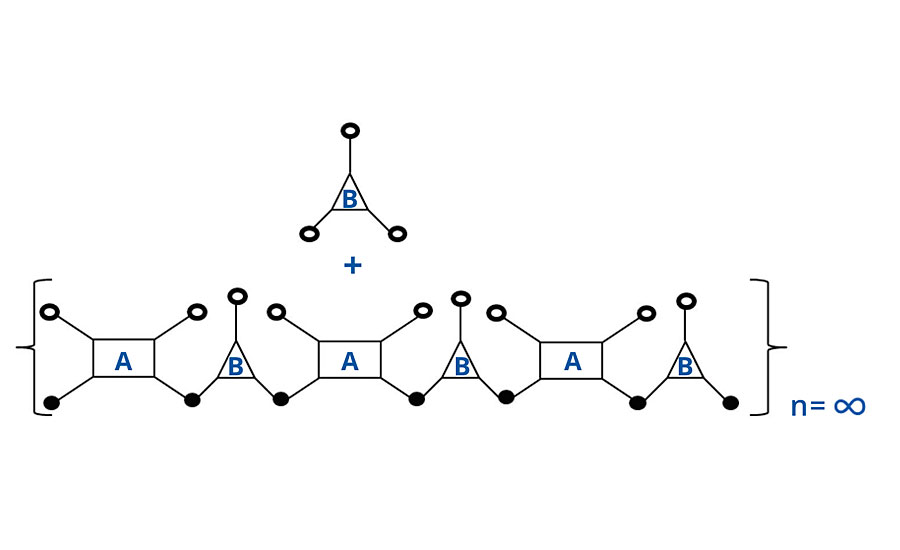
FIGURE 1 » Schematic of noninfinite chain for FA = 4, FB = 3.

As the last molecule of B is reacted with one of the pendant groups of A, infinite molecular weight is achieved and two reactive groups are consumed, as shown in Figure 2. However, analogous to the case above, one group is a “crosslinking” group (the third group of A) and only one of the two “extension” groups of B is consumed. Thus again, the algebra treats it differently (two groups are lost from B in the algebra), but the same result is achieved. That is either way, two additional groups are consumed to achieve infinite molecular weight (Table 4). In the next system we will include a monofunctional reactant or monomer.

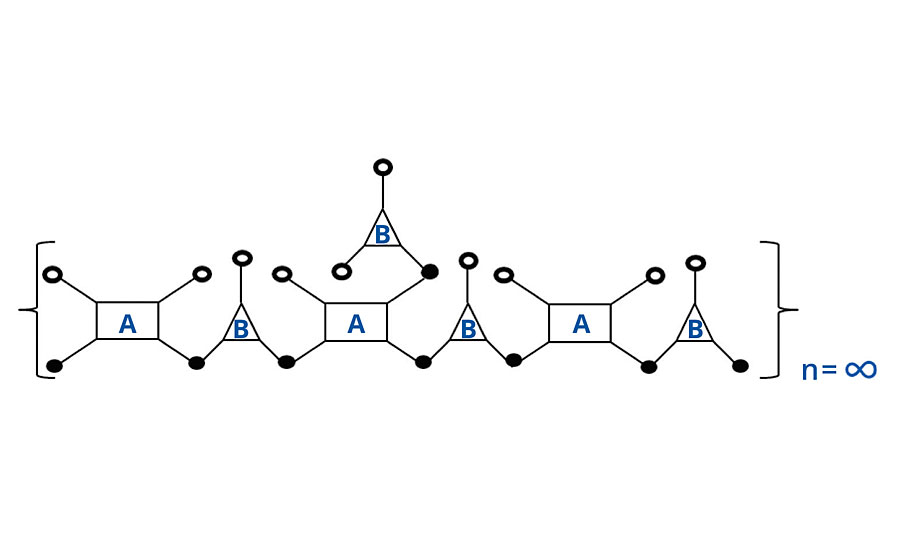
FIGURE 2 » Schematic of infinite chain for FA = 4, FB = 3.

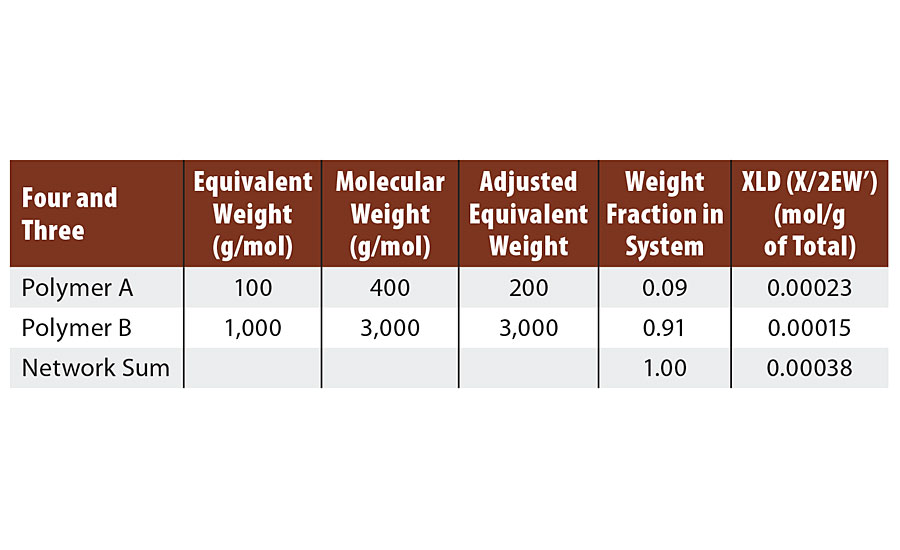
TABLE 4 » Calculated crosslink density of FA = 4, FB = 3.

Six Reactive Groups on Polymer A, Two Reactive Groups on Polymer B and One Reactive Group on Monomer C

This system was formulated so that both polymer B and monomer C were reactive with polymer A. We used a 50/50 mol ratio of polymer B and monomer C. We have recopied Table 3 with Table 5 for comparison. The first change to note is that the adjusted EW of the monomer C is a negative value since it actually removes potential crosslinks from the system.

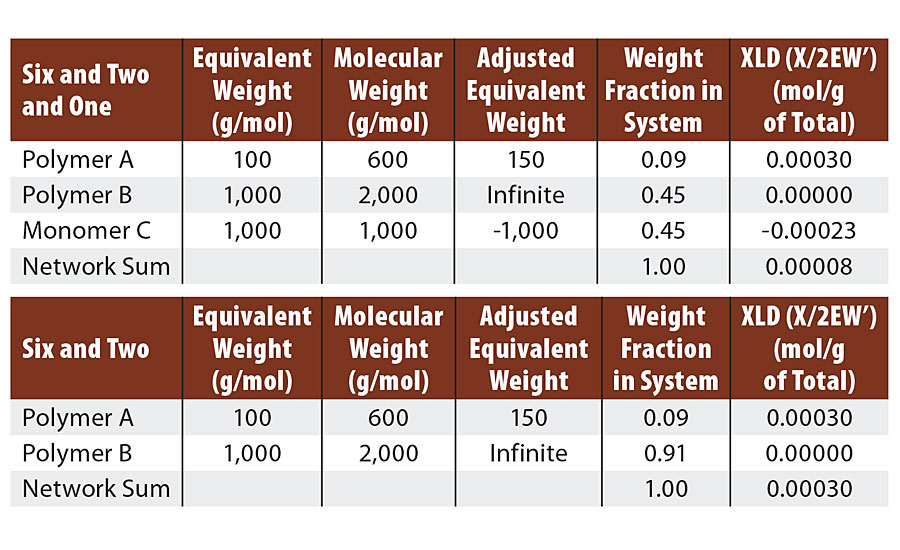
TABLE 5 » Calculated crosslink density of FA = 6, FB = 2, FC = 1. Compared to FA = 6, FB = 2 .

We can still react each melamine twice with diol as we did in the six and two example. This again leaves four unreacted groups on each melamine. In the case of the six and two example, each of these four groups formed ½ of a crosslink via a diol bridge for a total of two crosslinks per melamine. Here, three of the four remaining melamine groups react with the monomer C to yield no crosslinks. The last remaining melamine group reacts with a diol bridge to form ½ crosslink. So in the six and two and one case, we form ½ crosslink per melamine and in the six and two case we form two crosslinks per melamine. Thus we lose 75% of the crosslinks by addition of the monomer. This matches the results from the calculations below.

Many coatings chemists prefer to view the crosslinking in terms of Mc of the crosslinked film. Meaning the true Mc after adjustment for infinite molecular weight. This adjusted Mc’ = 2/XLD.

It is interesting now to consider noncontributing chain ends. In the Scanlan analysis, the probability of the “terminal” reactive group occurring some distance from the chain end was meticulously calculated. Although chain ends do indeed represent flaws or noncontributing segments in this theory of the crosslinked network, if the length or amount of these “noncontributing” segments is increased, then it only means that the length of the “contributing” segments are shorter. The number of crosslinks and the number of contributing or “elastically effective” chains do not change. Indeed the focus on the chain ends is somewhat arbitrary since even the pendant methyl groups on polyisoprene can be considered miniature dangling ends within in the chain. This same shortening principle applies to an acrylic polyol that uses butyl acrylate comonomer. The butyl groups are outside of the connecting chain.

Rather, the consideration of dangling segments determines how “elastically effective” the chains can be. In the case of Flory’s polyisoprene at 35k Daltons between crosslinks, elongations of up to 800% can be achieved. In systems where this Mc value is less than 500 Daltons, the strain to break is usually below 10%. Here the difference is representative of the difference in the “end-to-end” (or “crosslink to crosslink”) distances for the chains as they are extended from their random coil configuration to their fully extended configuration. This change in end-to-end distance is much larger for the higher molecular weight chains. Because this fully extended distance is determined by the number of atomic bonds that fall directly along the chain between the two ends, or crosslinks, it is here in the strain to break that the effect of groups outside of the connecting chain can have a dramatic effect. Thus such groups should be avoided in order to avoid brittleness, especially at high crosslink densities. Such groups include both prepolymer chain ends beyond the last reactive group on each chain as well as pendant groups inherent to the monomer structures used to form the prepolymers.

Returning now to the probability theory developed by Miller and Macosko. They modelled prepolymers of functionality f forming a crosslinked network. In Equation 49 from Reference 3, they list the “crosslink density” as the sum shown below:

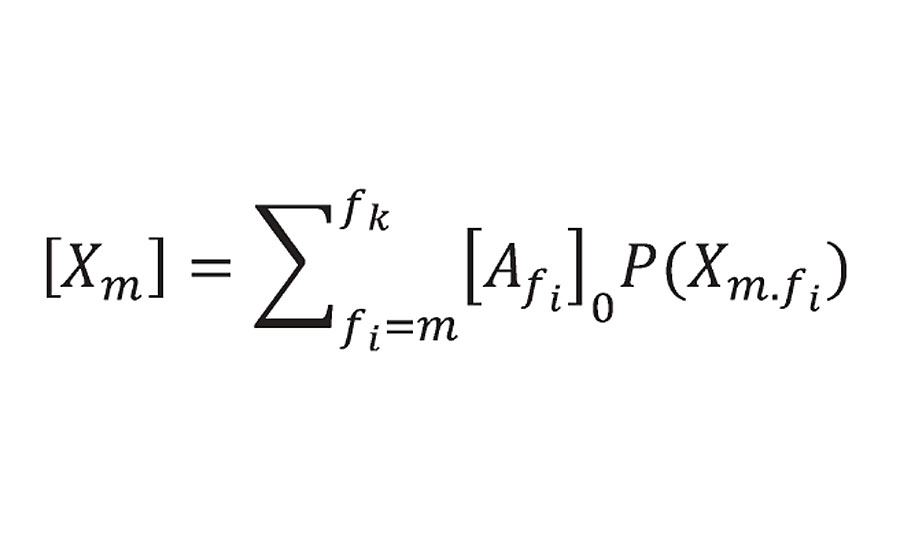
Equation 49 from Reference 3

He limited the summation to m = 3 or greater (i.e excluding prepolymers of f=2 or 1). P(X_m.fi) is the probability function and is 1.0 at 100% reaction. At this point X_m becomes the concentration of reactant groups from prepolymer of functionality f [A_fi]₀ where r is the density and Mc is the prepolymer equivalent weight. The factor of 2 accounting for the fact that each reactive group provide ½ of a crosslink. This is what we called bridges and not crosslinks because they do not account yet for infinite molecular weight. However, Miller and Macosko do account for infinite molecular weight (using a slightly different argument) in Equation 51 from Reference 3, where they calculate the number of effective chains as:

Equation 51 from Reference 3

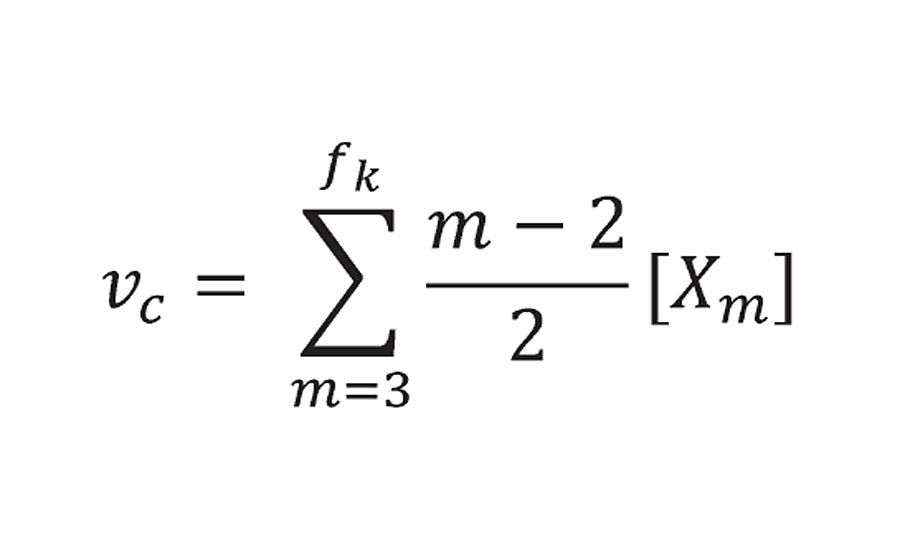
With the term m-2, they reduce the functionality of each prepolymer by 2. This is then equivalent to the correction that is made for the adjusted equivalent weight.

It is now clear that the Miller and Macosko treatment yields the same results as that shown in our work. The main difference is their definition of “crosslinks” to include chain extension bonds of reactants with f>2, but to exclude them for reactants of f=2 or f=1.

As noted in the introduction, Hill performed calculations both with and without the factor of (m-2) for the melamine resin. Although he correctly excluded crosslink contribution from the polyester diol. He used a single experimental point of a melamine diol system to validate the exclusion of the (m-2) factor for the melamine.

We will revisit this question. Table 6 compares the calculated crosslink densities for to different acrylic-melamine crosslinked systems where only the molecular weight of the acrylic was varied and therefore the degree of functionality (m-2). Both acrylic resins have an equivalent weigh just over 400 g/mol. The Mn of the higher molecular weight resin is just over 2,000 g/mol or a degree of functionality of about 5. The lower molecular weight acrylic resin is 1,200 Mn or a degree of functionality of about 3. The measured values for the high Mn acrylic resin is 1,325 mol/m³ while the low Mn resin measured at 620 mol/m³ by DMTA E’ minimum. The drop in crosslink density for the lower Mn resin is even greater than predicted. This may be due to the effect of the molecular weight distribution, which is not accounted for. Low molecular weight species can have a large effect and the distribution for this resin has some fractions with a degree of functionality of 1-2.

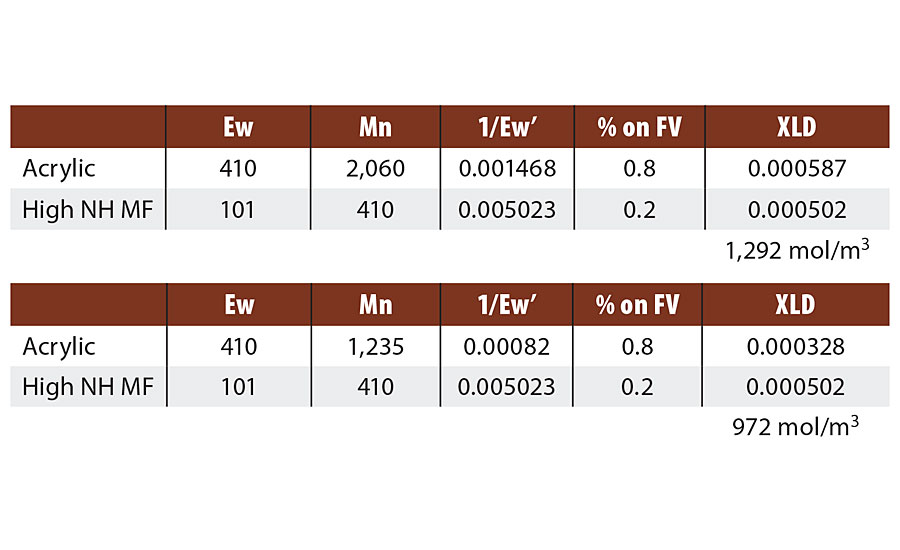
TABLE 6 » Calculated crosslink density for varied degree of functionality.

In addition, Flory evaluated a series of seven prepolymers spanning almost an order of magnitude in molecular weight. He achieved excellent correlation between the calculated value and the value measured from the elastic modulus in the rubber phase. His calculated values used the equation listed in the introduction. For a single self-crosslinking polymer, this is equivalent to our method. Flory made no corrections for dangling chain ends or for intrachain crosslinks.

Model for UV-Cured Systems – Kinetic Chain Length

In this next section, this aspect of acrylic chain length is further explored for the case of UV-cured systems. In particular, relating kinetic chain length to crosslink density. In UV-cured systems, kinetic chain length is used to describe the number of double bonds that polymerize in the chains. It can be limited by oxygen inhibition, recombination and by photoinitiator levels. It is often discussed, by it cannot itself be easily measured except via crosslink density. Its effect can be easily overestimated, as we will show.

We will look at the polymerization of several polyacrylate oligomers. In the formation of the chain, multiple groups react and each group reacts with two others forming (at least) two half crosslinks. The initiator has been left out below for simplicity in the chain with a kinetic chain length of n=5 (Figure 3).

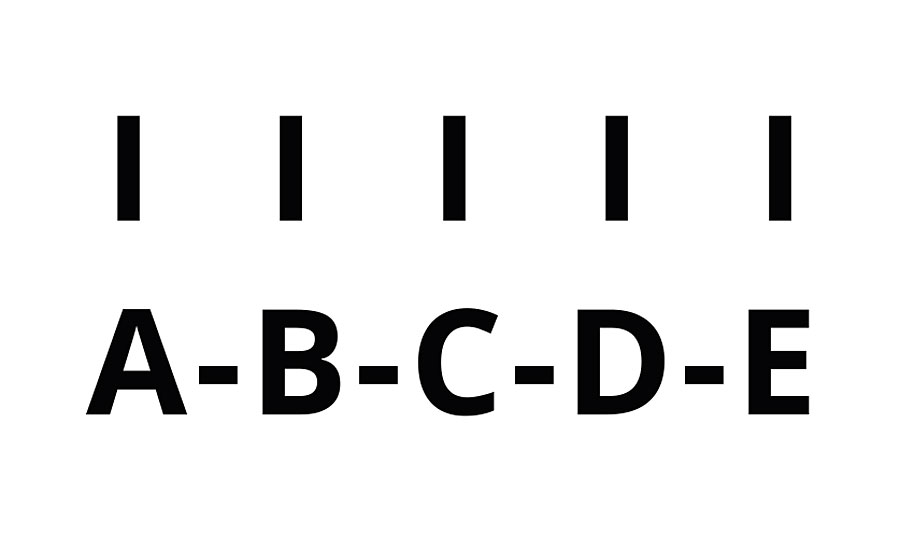
FIGURE 3 » Schematic of UV-cured polymer n = 5.

Here oligomer A is crosslinked not only to B, but also to C, D and E. Likewise, oligomer B is crosslinked to C, D and E. Thus, the total number of crosslinks is given by Equation 5.

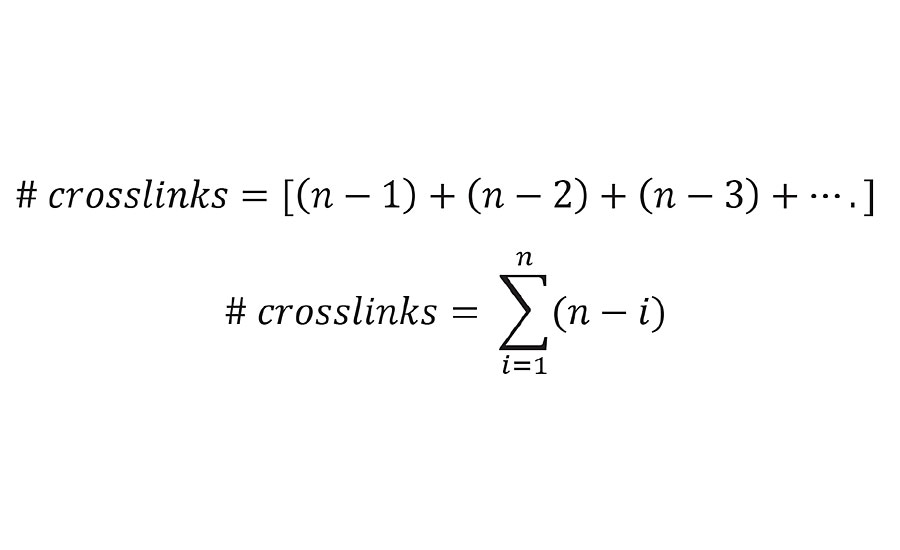
EQUATION 5 » Number of crosslinks from kinetic chain length (n).

We then used this to calculate the crosslink density of several polyacrylate oligomers (Figure 4). Hexanediol diacrylate (HDODA), hexamethylene diisocyanate trimer with three mols of hydroxyethyl acrylate (HDI-HEA), trimethylolpropane triacrylate (TMPTA) and pentaerythritol tetraacryate (PETA). Since this will be a purely theoretical study, we used the molecular weights of the model compounds in the calculations. Because we are more interested in the effect at longer chain length, we only removed one group per molecule for the infinite molecular weight formation. This is obviously incorrect at low chain lengths.

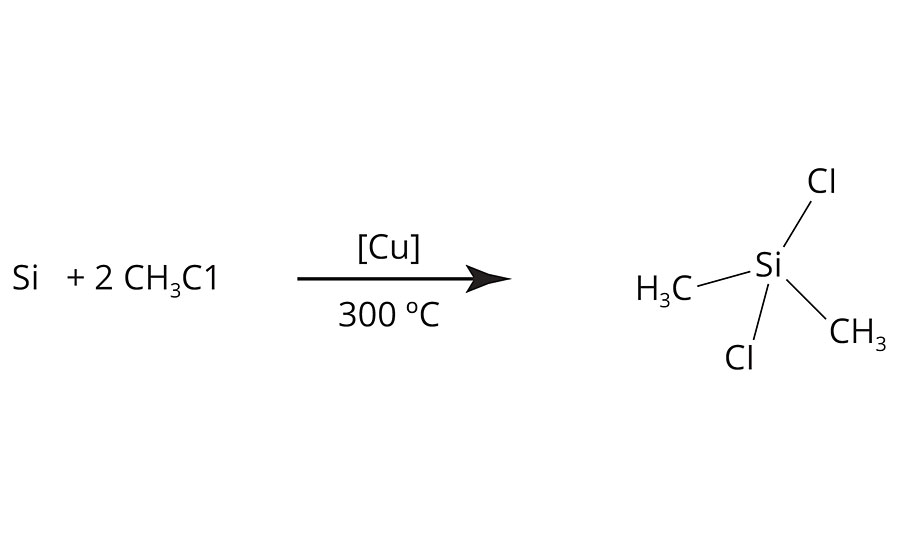
FIGURE 4 » Crosslink density vs. chain length – simple model.

Here we see that crosslink density rises linearly with kinetic chain length to achieve astronomical values. However, this model does not account for the fact that there is a finite distance, or Mc, between monomer A and monomer E in the chain shown above. In particular, each monomer has two CH₂ groups or 28 Daltons. If we adjust for this factor of Mc, then we see that the crosslink density levels off at higher kinetic chain lengths, as shown in Figure 5.

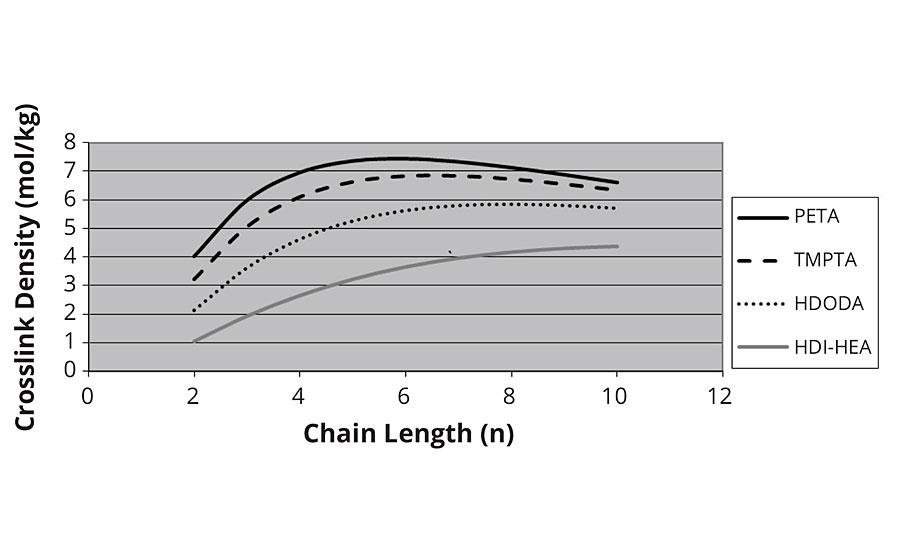
FIGURE 5 » Crosslink density vs. chain length – adjusted for Mc.

However, the model here is incorrect in that more than one group is required to form infinite molecular weight at low values of n, and the drop in crosslink density at higher values of n is obviously not correct.

It was at this point we decided to calculate the chains as “prepolymers” of acrylic acid and crosslink them with the polyols (e.g. hexane diol, trimethylolpropane etc.). Essentially using the same model as for the thermal crosslinking developed in the first section. Here we confirm the levelling off of crosslink density with higher kinetic chain lengths, as shown in Figure 6. We also see that the crosslink density of the diacrylate correctly goes to zero as the chain length approaches two for HDODA.

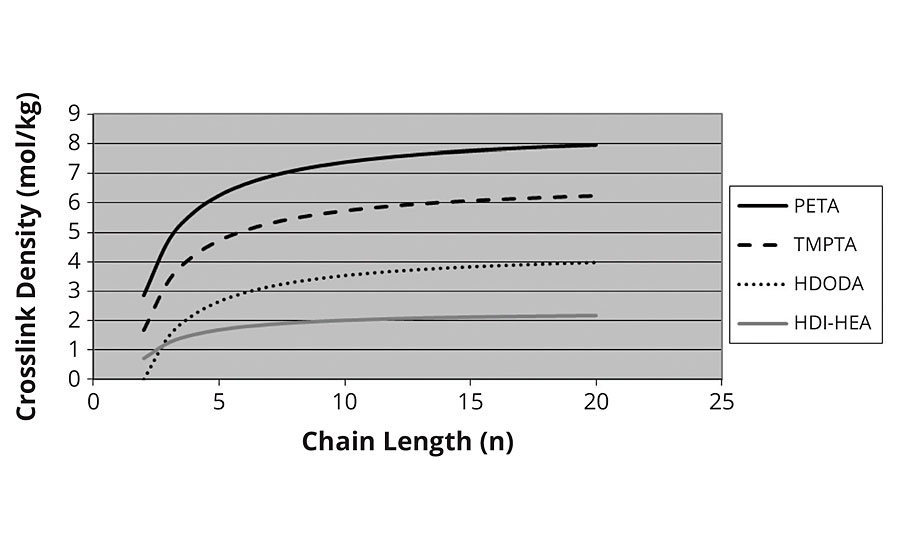
FIGURE 6 » Crosslink density vs. chain length – thermal model.

Conclusions

We have demonstrated the equivalence of our simple calculations for crosslink density to more sophisticated methods developed by others. By virtue of the method’s simplicity it has been easily extended to more complicated UV-curing systems and serves to easily determine the effects of prepolymer architecture on the crosslink density in the cured film.

References

1   Flory, P.J. Chem. Revs., 35, 51 (1944) 51-75.

2   Scanlan, J. J. Polymer Sci., 43, (1960) 501-508.

3   Miller, D.R.; Macosko, C.W. Macromolecules, 9, 2 (1976) 206-211.

4   Graessley, W.W. Adv. Poly. Sci., 16 (1974) 108.

5   Hill, L.W. Prog. Org. Coatings, 31 (1997), 235-243.

6   Berger, J.; Huntjens, F. Die Angewandte Makromolekular Chemie, 76/77, (1979) 109-122.

7   Chen, J.S.; Ober, C.K.; Poliks, M.D.; Zhang, Y.; Weisner, U.; Cohen, C. Polymer, 45 (2004) 1939-1950

8   Ahagon, A.; Gent, A.N.; J.Poly. Sci., Poly.Physics Ed., 13 (1975) 1903-1911.

9   Levita, G.; De Petris, S.; Marchetti, A.; Lazzeri, A. J. Mat. Sci., 26 (1991) 2348-2352.

10 Pruitt, L.A. Conventional and Cross-Linked Polyethylene Properties. p 353-360 In: Bellemans J., Ries M.D., Victor J.M. (eds) Total Knee Arthroplasty. Springer, Berlin, Heidelberg, (2005).